Embedding을 저장하는 VectorDB 그리고 벡터 유사도 검색 Indexing
정형데이터 뿐만 아니라 텍스트 이미지 비정형 데이터, 더 나아가 LLM까지 앞으로 VectorDB를 빼놓을수가 없게 되었다.
우리도 VectorDB를 사용하고 있으며, 벡터간의 유사도 검색으로 다양한 서비스에 적용하고 있다.
이번글에서는 기본적인 vector와 embedding 그리고 vectorDB의 이론적인 개념에 대해서 살펴보려고 한다.

Vector란?
고등학교 수학에서 <기하와 벡터> 때 배웠던 그 벡터 맞다.
간략하게 기하학에서 벡터는 '크기'와 '방향'을 함께 가지는 물리량을 벡터라고 표현했다.
화살표 방향이 벡터의 방향이고, 화살표 길이가 크기가 되었다.


그렇다면 DataScience에서는 여러 의미의 데이터들을 특정한 순서대로 모아둔 데이터 레코드를 벡터라고 부르고,
이러한 벡터가 여러개 있는 데이터의 집합은 행렬(Matrix)이라 부른다.

그래서 텍스트나 이미지 같은 비정형 데이터들을 데이터화 하기 위해 벡터로 변환을 하고,
그 벡터를 통해 데이터 뭉치들에서 패턴을 파악하는 데이터 분석을 할 수 있는 것이다.
이때 벡터로 변환하는 작업을 임베딩(Embedding)이라고 한다.
Embedding 이란?
One-Hot Encoding
간단하게 단어를 숫자 벡터화 하는 작업이다.
정수인코딩(Integer Encoding)으로 단어를 빈도순으로 정렬하고 빈도수가 낮은 숫자부터 정수를 부여하는것이다.

하지만 단어의 개수가 늘어날수록 벡터를 저장하기 위한 공간이 계속 늘어나 공간활용에 비효율적이라는 단점이 있다.
또한 각 단어의 존재를 쉽게 확인할수 잇지만, 각 단어의 관계성을 파악하기는 힘들다.
Word Embdding
위의 단점을 보완하기 위해 단어간의 의미적 유사성을 벡터화 하는 작업이다. 이렇게 표현된 벡터는 임베딩 벡터라고 부른다.
비슷한 내용의 단어를 벡터화 시켜서 그 벡터들은 유사한 값을 가지게 되는 것이다. 그러면 단어의 의미를 여러차원에 분산하여 표현하여 공간활용에도 제약이 덜하고, 유의미한 유사도를 계산 할 수도 있어서 관계성도 파악할수 있다.

사람이 임베딩 벡터를 확인하고 의미를 파악하긴 어렵지만, 임베딩간의 거리를 계산하면 이들의 의미적 관계를 파악할수 있다.
이때 이러한 임베딩 벡터 결과를 저장하고 쿼리하기 위한 database가 필요하게 되었다.
VectorDB란?
'임베딩 벡터'을 저장하고 조회하기 위한 데이터베이스.
기존 RDBMS는 쿼리와 정확히 일치하는 행을 찾는 반면, VectoDB는 벡터간의 거리나 유사도를 기반으로 가장 유사한 벡터를 찾는다.

그러나 벡터사이의 거리 메트릭을 비교하는건 너무 많은 시간이 걸린다.
그래서 벡터를 빠르게 쿼리하는 것도 중요하고, 정확한 결과를 탐색하는것 또한 중요한 포인트이다.
결국 필연적으로 정확도와 탐색 속도 사이의 tradeOff가 생기기 마련인데, 이를 조절하기 위한 Indexing 알고리즘을 적용한다.
Vector Indexing 기법
1.Flat Index
별도의 인덱싱 기법 없이 벡터를 저장하는 방법이다.
모든 벡터들과 유사도를 계산해 가장 높은 유사도를 지닌 벡터를 찾는다.
일반적으로 10000~50000개 정도의 벡터에서 적당한 성능과 높은 정확성을 얻을수 있다고 한다.
하지만 실제로 이렇게 사용한다면 벡터 데이터가 더 많아 탐색 속도가 느려질 것 이다.
2.Random Projection
랜덤한 벡터를 만들어서 원래 벡터와의 내적을 시켜서 차원을 줄이는 방법이다.
원래 벡터와의 유사성도 유지할수 있고 고차원의 원래 벡터보다 탐색속도가 빠를수 있다고 한다.
하지만 Approxiamtion이기 때문에 정확도는 보다 떨어질수 있을 것이다.
3.PQ (Product Quantization)
원래 벡터를 균등하게 몇개의 서브벡터로 쪼개고, 각 서브벡터들을 Quantization하여 크기를 줄이는 방법이다.
빠르고 정확도도 좋으며 큰 데이터셋에서 사용하기 좋은 기법이라고 한다. Quantiztion으로 값을 표현하는데 사용하는 bit수를 줄이기 때문에 메모리 사용량도 적고, 탐색 속도도 빠르다.
하지만 근본적으로 표현하는 숫자의 범위를 제한하는 방법이기 때문에 정확도는 다소 떨어질수 있다.
4.LSH (Locality-Sensitive Hashing)
원래 벡터를 hashing 함수에 한번 돌려서 bucket에 매핑하고, bucket에서 비교하여 찾는 방법이다.
유사도 검색을 할때도 쿼리문에 대한 벡터를 동일한 해싱함수를 사용해서 같은 버킷에 있는 벡터들하고만 비교하여 찾는다.
전체 데이터가 아니라 버킷에 있는 데이터안에서만 찾기 때문에 탐색속도가 빠르다.
하지만 버킷이 많을수록 정확도가 높아지겟지만, 더 많은 메모리가 필요하게 된다.
5.HNSW (Hierarchical Navigable Small World grahp)
원래 벡터를 가지고 N개의 레이어를 가진 그래프를 생성하고, 그래프를 기반으로 가장 가까운(유사도가 높은)결과를 찾아내는 방법이다.
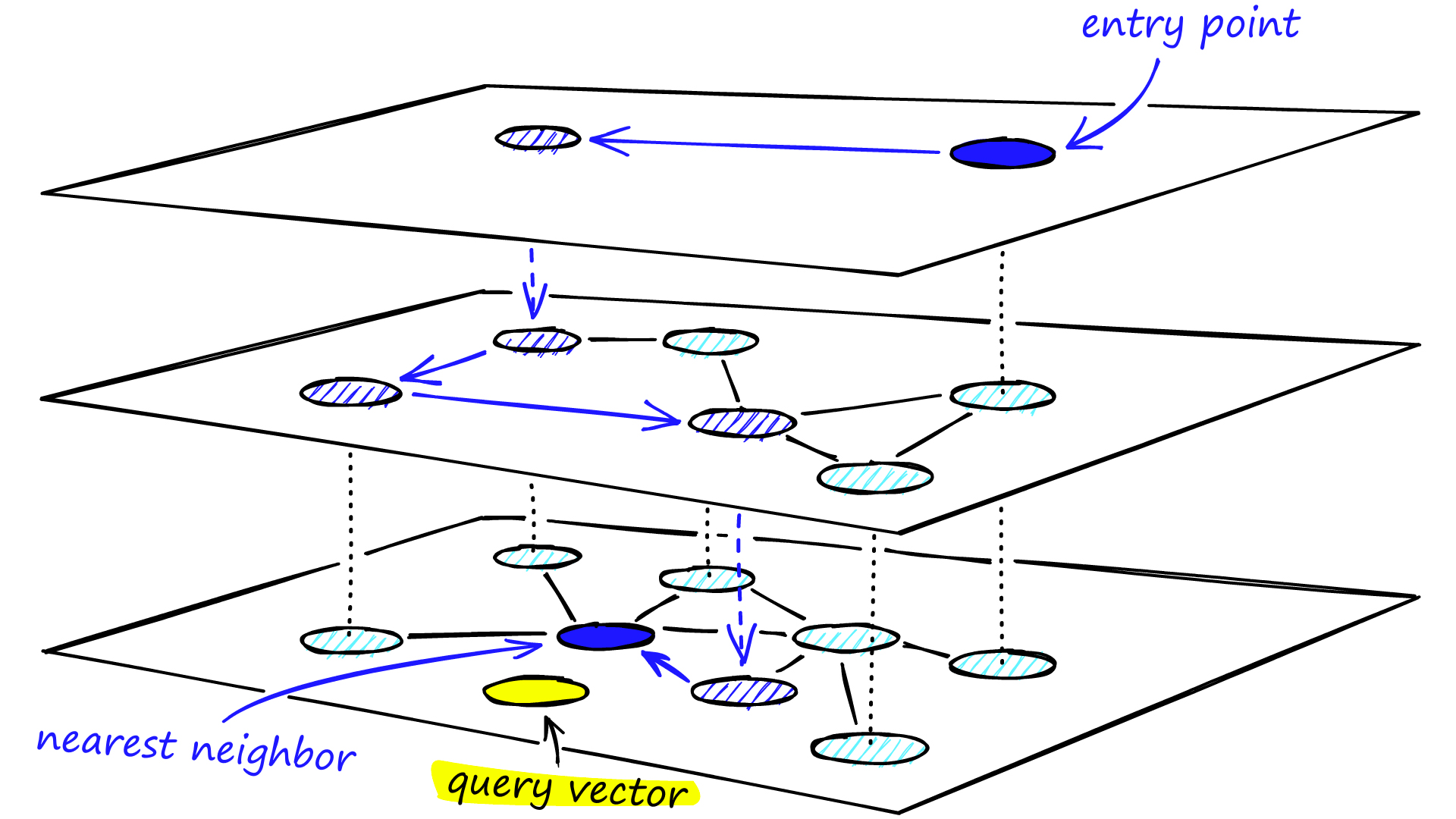
아래와 같은 로직으로 유사도를 알아낼 수 있다.
1.최상위 레이어의 임의의 노드에서 탐색을 시작하고, 가까운 노드로 이동한다.
2.현재 레이어에서 더 가까워질수 없다면 하위 레이어로 이동한다.
3.모든 벡터가 존재하는 최하위 레이어에 도달할때까지 1,2를 반복한다.
4.쿼리벡터와 유사도가 가장 높은 벡터를 발견한다.
속도와 정확도가 높아 큰 데이터셋에서 사용하기 좋은 기법이며, 검색 대상의 그래프를 어떻게 구성할것이냐가 검색 성능에 영향을 미친다.
그리고 모든 데이터가 아니라 그래프를 통해 검색을 하기 때문에 검색속도도 빠르다.
하지만 속도와 정확도 사이의 tradeoff 때문에 아래의 파라미터를 통해 조절해야한다.
- m : 하나의 노드가 가지는 이웃 노드의 개수
값이 클수록 그래프가 촘촘해진다 -> 정확도는 높아지지만, 검색 속도 느려짐, 인덱스 크기(메모리) 증가 - ef_construction : 그래프 구성시, 참조하려고 하는 이웃의 범위
값이 클수록 그래프 신뢰도가 높아짐(임계치존재) -> 정확도는 높아지지만, 검색 속도 느려짐. - ef_search(ef): 검색시, 참조하려고 하는 이웃의 범위
클수록 탐색하는 노드가 많아짐(해당값 만큼 탐색) -> 정확도는 높아지지만, 검색 속도 느려짐
6.IVF(Inverted file index)
clustering 알고리즘으로 n개의 cluster로 나누고, cluster에 벡터들의 위치를 매핑하여 저장한 inverted list를 통해 찾는 방법이다.
검색 쿼리가 주어지면 그 쿼리가 포함된 클러스터를 찾고, 해당 클러스터에서는 책에 있는 index처럼 문서의 위치를 매핑하여 저장한 값을 보고 벡터들에 대한 검색을 할 수 있다.
일반적으로 LSH, HNSW, IVF 알고리즘은 모든 데이터가 아니라 일부만 확인한다는 점에서 검색 공간의 활용도가 높다.
즉, 검색 속도 빠르다. 그러나 검색결과의 정확도와는 tradeoff이기 때문에 이를 위한 파라미터 조정이 필요하다.
Vector Querying
indexing을 어떻게 하느냐에 따라 검색방법도 달라진다.
검색 쿼리가 들어왔을때 설정한 indexing 알고리즘에 따라 유사도 검색을 한다. 크게 세가지 방법이 있다.
1.Cosine Similarity
두 벡터간의 각도를 측정하는 방법.
1에 가까울수록 유사한 벡터이고, -1에 가까울수록 정반대의 벡터이다.
2.Euclidean Distance (L2)
두 벡터간의 직선거리를 측정하는 방법.
0에 가까울수록 유사한 벡터, 값이 클수록 정반대의 벡터이다.
3.Dot Product (내적)
두 벡터간의 내적을 측정하는 방법.
양수는 같은 방향, 음수는 반대방향의 벡터이다.
다음에는 실제로 이러한 내용을 적용해보기 위해 직접 사용한 vector 라이브러리 (faiss,hnswlib)와
직접 로컬에서 vectorDB를 설치하여 인덱싱과 쿼리에 대해서 알아보고자한다!

출처
https://gruuuuu.github.io/ai/vector-store/#1-indexing
호다닥 톺아보는 VectorDB 기초
Overview 지난 게시글에서는 Vector란 무엇인가?에 대해서 작성했었습니다.
gruuuuu.github.io
벡터 데이터베이스 소개 | 음악 검색 기능은 어떻게 만드는 걸까?
벡터 임베딩(Vector Embedding)은 머신 러닝의 핵심 요소로 이미지, 음성, 단백질 분자 구조 등의 비정형 데이터를 일련의 벡터 공간으로 표현하는 기법이다. 비정형 데이터를 벡터로 표현하고 나면
medium.com
https://techblog.woowahan.com/17383/
실시간 반응형 추천 개발 일지 #1. 프로젝트 소개 | 우아한형제들 기술블로그
실시간 반응형 추천 개발 일지 #1. 프로젝트 소개
techblog.woowahan.com